Fractal Explorer

Date Written: October 11, 2023; Last Modified: October 11, 2023

When I was in high school, I used Java to create Newton fractals. The goal was originally to make a music visualiser, but I didn’t really know what I was doing well enough and settled for a simple fractal generator. The issue was that I wrote a single-threaded fractal renderer, which shaded pixels one at a time. At a resolution of even 144p, this is painfully slow, and I wasn’t able to adapt it to make animations.

It’s been perhaps 5 years since I made that project, and on a recent family vacation, I decided to revamp it and make it better - a lot better. Hence, this project was born! I had intended it to be a short one-day coding sprint that made something marginally cool at the end, but there ended up being some very cool mathematics and concepts that I wanted to share.

Preliminaries: How to make a Fractal

You might be familiar with the Mandelbrot set, especially since there are so many videos of it. I remember watching several Mandelbrot set zoom videos like this one (I found some stranger videos about it too). In principle, it’s generated by a pretty simple procedure: start at some point in the complex plane $z$, then see what happens to the sequence $z, f(z), f(f(z)), f(f(f(z))), \ldots$. The Mandelbrot set uses the starting point $z=0$ and iterated function $f:z\mapsto z^2+c$. This constant $c$ is determined by the location of each pixel on the screen, and the pixels are coloured based on the behaviour of the above sequence.

Newton fractals use a similar principal of creating a sequence and shading pixels based on the behaivour of said sequence; 3Blue1Brown made a great video describing how they work. Nevertheless, I’ll provide my own explanation for completeness.

Let’s say you have some holomorphic function $f:\mathbb C\to\mathbb C$. A question one could ask is: what are the roots of $f$? In general, this question is impossible to answer, so the next best thing is numerical approximation. Newton’s method provides an algorithm to do this.

First, “guess” a root $z_0$. We may use a linear approximation \[f(z)\approx f\left(z_0\right)+f’\left(z_0\right)\left(z-z_0\right).\] This approximation is pretty awful, but it’s better than nothing. If we want $f(z)=0$, we may use the above approximation to improve our guess: \[f\left(z_0\right)+f’\left(z_0\right)\left(z-z_0\right)=0\implies z=z_0-\frac{f\left(z_0\right)}{f’\left(z_0\right)}=:z_1.\] Chances are, $z_1$ is not a root of $f$, but it’s typically a little closer than whatever our initial guess $z_0$ was. This lets us approximate using $z_1$ instead of $z_0$ and define $z_2$, then repeat ad infinitum. Eventually, this sequence will (hopefully) converge to a root. (Intuitively, we’re “tracing” the tangent line down to the horizontal axis.)

There are several practical issues with this method:

You may be dividing by zero: if $f’\left(z_n\right)$ is ever zero, $z_{n+1}$ won’t be well-defined.
The sequence $z_n$ may not converge at all: with sufficiently pathological functions or sufficiently poor starting guesses, the sequence could blow up to infinity (even without division by zero!), or it could even oscillate between several repeated points that aren’t roots (the Wikipedia page provides an example).
If $f$ has multiple roots, you have no clue which root you’ll end up at.

As far as making fractals goes, however, issue #3 becomes crucial feature #1: it turns out that shading the complex plane according to the root produced by Newton’s method produces a fractal. Add some shading based on how long it takes to converge and here’s what you get:

$image An example of a Newton fractal$

I think the star-shaped regions are cute.

For the rest of this article, we’ll understand that the function used to produce these Newton fractals is a polynomial. This is advantageous for 2 reasons: first, it’s easy to compute; second, its derivative is easy to compute (for computers). These are not true for arbitrary functions.

Animation, and a Question for Complex Dynamics

You probably scrolled past the above image pretty quickly, and that’s probably because you, like me and many others, have an infinitesimal attention span. Things are far more interesting when they move and change, so a natural question to ask is, how the heck should we do that?

My idea happens to work out very nicely: small changes in the coefficients of the polynomial result in small changes in the resulting Newton fractal. By animating the coefficients of the polynomial, you end up with a smooth animation of the fractal itself.

Wait what? It is not at all obvious to me that a perturbation of the coefficients results in a perturbation of the fractal. It seems like what’s happening is that near locations where the fractal is “simple”, the perturbation of the polynomial (much like a small perturbation of the location) results in not much of a change in the fractal itself. Near locations where the fractal is chaotic and “fractal-like”, the resolution isn’t high enough for us to notice the significant changes in behaviour. If you know much about complex dynamics and are willing to talk about this, please contact me!

The Procedurally Generated Animations

The ultimate question is, how does one randomly generate an animation of the coefficients? If $n=\deg f$, we are asking for a way to get a random walk in $n+1$ dimensions. This is not terribly hard: successively generate random points, then linearly interpolate between them.

I did try this, and it produced rather jagged animations. The question is then: how does one randomly generate a smooth random walk?

The idea of successively generating random “waypoints” is not a bad one, as one can perhaps fit splines through these points. I also thought about connecting “waypoints” using Bézier curves. Both of these ideas had the drawback that one needs to generate several “waypoints” at a time to ensure the path would pass through each one smoothly. This was too much for me to handle.

Instead, I decided the problem would be better tackled by animating each coefficient independently and smoothly. So, we should ask, “how can one randomly generated a single-variable real-valued smooth function?”

Let $c(t)$ be any coefficient of the polynomial as a function of time, to be constructed later. What a linear interpolation between waypoints essentially does is it makes $c’(t)$ a piecewise constant function. This then forces $c(t)$ to be piecewise linear, which we can recognise as non-smooth due to the “corners”. However, if we go one step forward and decide to make $c’’(t)$ a piecewise constant function, $c(t)$ will be once continuously differentiable, which for most people is “smooth enough”. In general, deciding $c ^{(k)}(t)$ as a piecewise constant function for $k\geq 2$ makes $c$ a $k-1$-times continuously differentiable function. By randomly picking a new value for $c ^{(k)}(t)$ every second, for instance, this creates the effect of a random walk, more or less. One can perhaps imagine this method as “integrating a 1-D random walk” a few times to smooth it out.

I tried this method at first, but a significant issue came up. Using the $k=2$ scenario, one may start with a value of $c’(0)=1$ and randomly choose $c’’(t)=1.5$ for $t\in [0, 1]$, then $c’’(t)=0.8$ for $t\in[1,2]$, and finally $c’’(t)=2.4$ for $t\in[2, 3]$. This leaves $c’(3)=5.7$. Most likely, $c’$ will stay positive for quite a long time after this. The resulting graph of $c$ will be an uninteresting squiggle that’s monotonic. The coefficients of the polynomial $f$ under this scheme thus grow very large in one direction, ultimately producing uninteresting fractals that don’t change much relative to each other.

Well, I implemented this strategy essentially using a finite differencing method. See Coefficients.cpp for the implementation details. An advantage of this was that I was able to “tune” the coefficients by multiplying by a factor slightly smaller than 1. If we force $c ^{(k)}(t)$ to stay bounded, which we can totally do, this multiplicative factor prevents $c ^{(k-1)}(t)$ from being too large, and this ultimately bounds the first $k$ derivatives of $c$, including $c$ itself.

Here are a couple of sample functions that this modified method was able to create. They are “plotted” as single-variable functions of time, with the axes and scales omitted because they’re ugly.

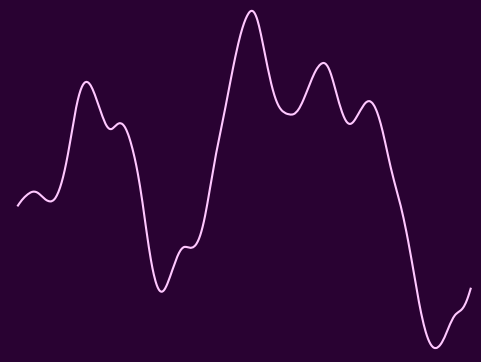They actually seem reasonably random and smooth at the same time. Here are some random walks for comparison:

Surprisingly, the “smooth walks” that I generated do resemble the large-scale shape of random walks, yet they’re not jittery at all in comparison.

I’m in a course on probability theory this year, and hopefully we’ll be learning about stochastic calculus, which seems like a great theory that can better explain and describe why this (frankly naïve) scheme makes “vaguely random walks”. Perhaps I’ll revisit this project after finishing the course to see if I have a better and more formal description of what I’m really doing.

Results

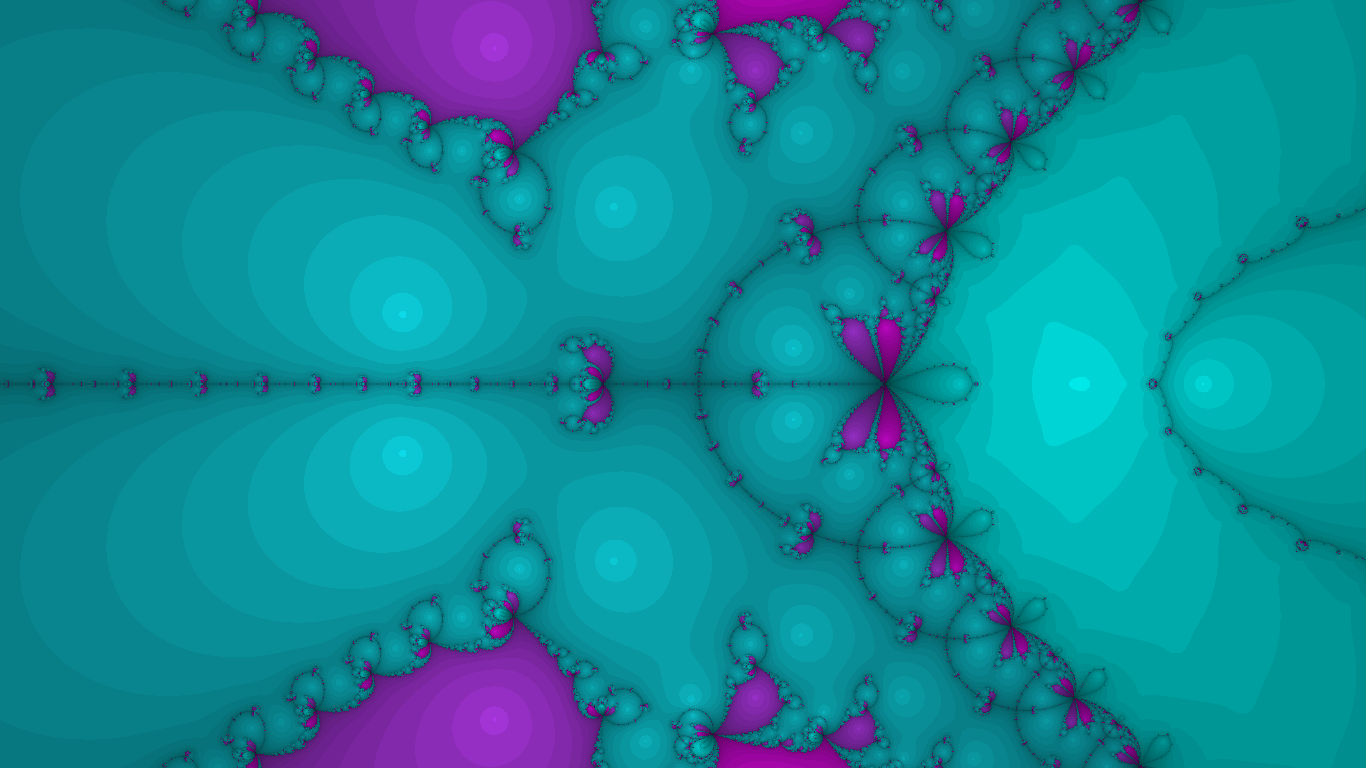
I can’t make this post without showing off how it turned out. I don’t have a computer good enough to take good screen recordings that capture the beauty of the animation. Here’s nine screenshots instead. If you open them all in separate tabs and Ctrl-tab through them very quickly, it might look like it’s animated. I’d definitely recommend opening these up in a new tab to get a better look.

This does look far better when it’s animated. My computer is rather trashy, so it can’t support a very high resolution animation; the moving parts make the poor resolution look smooth, however. Please build the project yourself and try it out!

Hunter Liu's Website